선형대수 기저와 차원

일차결합

위의 행렬을 쉽게 표기해 보자. (0.0)에서 -2만큼 오른쪽으로 3만큼 위로 움직였다.

이를 벡터로 표현하자면 (-2, 3) = -2e₁ + 3e₂

를 파란색을 기본단위 벡터 라고한다. 이러한 모양을 가리켜 일차결합이라고 한다. e₁ (1.0) e₂ (0.1)을 의미한다. 3차원이라면 e₃이 있을것이다.

일차결합의 정의는

A₁ , A₂ , …, A_n ∈ V (벡터공간)

k₁ , k₂ , …, k_n ∈ R (실수체) 두 가지를 곱

k₁A₁ + k₂A₂+ …+ k_nA_n

이러한 식은 다음과 같다. 백터들의 일차결합이란 그 앞에 스칼라를 곱해주고 다 더해주면 된다.

벡터의 일차결합의 표현

Rⁿ 벡터공간의 한 원소 C=(c,c,...c)

A₁=(a₁₁,a₁₂,...,a_1n) , A₂=(a₂₁,a₂₂,...,a_2n), A_m=(a_m1,a_m2,...,a_mn)

C=k₁A₁+k₂A₂+...+k_mA_m

파란 줄의 벡터를 횡으로 놓고 열백터로 내려쓰고 k스칼라를 곱하면 C를 일차결합으로 나타낼 수 있다.

결국 C, A₁ , A₂ , …, A_m ∈ Rⁿ 일 때, C가 A₁ , A₂ , …, A_m의 일차결합으로 표현가능하다. ⇔ 행렬방정식 AK = C의 해가 존재한다. 

비슷한 것으로 rank(A) = rank (A|C)

 

벡터들의 일차 독립성

종속성과 독립성

벡터들의 일차독립과 일차종속

α = {A₁, A₂ , …, A_n} ⊂ V (벡터공간) , k₁, k₂, …, k_n ∈ R (실수체)

① ∀k_i = 0 ⇒ α는 일차독립
② ∃k_j ≠ 0 ⇒ α는 일차종속

생각해 보자 만약에 A₃=k₁A₁+k₂A₂라고 한다면 A를 반대항으로 옮기면 영벡터가 되겠다. 그럼 k1A1+k2 A2+(-1) A3=O 가 된다. 위의 식과 비슷하게 나온다. 그럼 에이원 있고 에이투 있고 에이쓰리가 있다면 0이 아닌 계수가 최소한 하나는 존재한다고 말할 수 있다.

벡터들의 일차종속

n개의 벡터 A₁, A₂, …, A_n 이 일차종속이기 위한 필요충분조건은 어떤 1개의 벡터를 나머지 n - 1개의 벡터들의 일차결합으로 나타낼 수 있다는 것이다.

 

n개의 벡터 A₁, A₂, …, A_n 이 일차독립이기 위한 필요충분조건은 어떤 벡터도 나머지 n - 1개의 벡터들의 일차결합으로 나타낼 수 없다는 것이다.

 

일차독립과 행렬식

R_n 벡터공간에서 n개의 벡터 A₁, A₂, …, A_n이 일차독립이기 위한 필요충분조건은 벡터들을 열로 나타내어 만든 행렬식이 0이 아닌 것이다.

각각의 벡터 A를 열벡터로 두고, 열과 행이 모두 n개인 것임으로 정방행렬이 된다. 이렇게 생긴 행렬식이 0이 아니라면 일차 독립이 된다.

Rⁿ벡터들의 일차 종속

Rⁿ 벡터공간에서의 벡터의 개수가 n보다 많다면 이경우 벡터는 항상 일차종속이다.

알투 공간에서 벡터가 세 가지가 있다면 일차 종속이 된다. 식을 계산 해보면 계수중에 0이 아닌 게 나온다.

 

ixj소행렬

A가 mxn 행렬이라고 할 때 행렬 A에서 i개의 행을 뽑아서 ixn행렬을 만들고, 여기다가 j개의 열을 뽑아서 만든 ixj의 행렬을 행렬 A의 ixj의 소행렬이라고 한다. 

 

Rⁿ 벡터공간에서 m개(m <n)의 벡터 A₁, A₂, …, A_m에 대하여 이 벡터들을 열로 써서 만든 nxm행렬을 A= ( ₁, A₂, …, A_m )이라고 한다면, ₁, A₂, …, A_m이 일차 독립이 되기 위한 필요충분조건은 행렬 A의 mxm소행렬 중 적어도 하나는 행렬식이 0이 아닌것이 된다. 쉽게 위의 소행렬중 행렬식값이 이 아닌 게 나온다면 일차독립이다.

벡터공간의 기저와 차원

벡터공간에서 기저

벡터공간 V의 n개의 O아닌 벡터들의 집합 α = { ₁, A₂, …, A_n }이 다음 두 조건을 만족할 때 α를 V의 기저라 한다.
(1) α의 원소는 일차독립이다.
(2) V의 임의의 원소는 A₁, A₂, …, A_n 의 일차결합으로 표시된다.
∀A ∈ V, ∀k_i ∈  F,

A = 그림

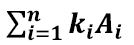
 V = sp(₁, A₂, …, A_n)